20250503 LeetCode每日一题——1007. 行相等的最少多米诺旋转

1007. 行相等的最少多米诺旋转

在一排多米诺骨牌中，tops[i] 和 bottoms[i] 分别代表第 i 个多米诺骨牌的上半部分和下半部分。（一个多米诺是两个从 1 到 6 的数字同列平铺形成的 —— 该平铺的每一半上都有一个数字。）

我们可以旋转第 i 张多米诺，使得 tops[i] 和 bottoms[i] 的值交换。

返回能使 tops 中所有值或者 bottoms 中所有值都相同的最小旋转次数。

如果无法做到，返回 -1.

示例 1：

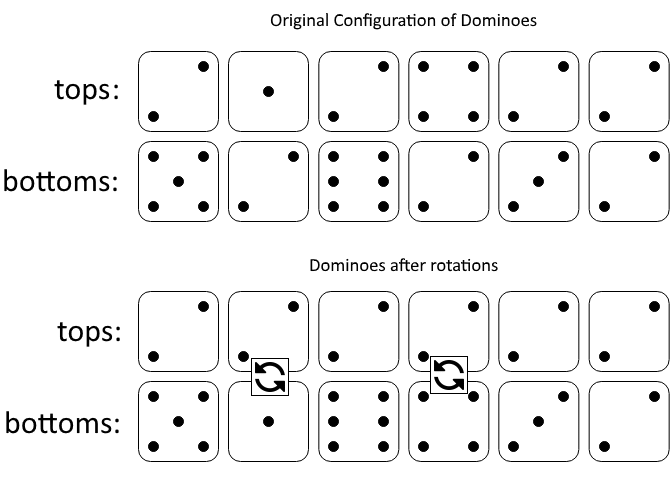
输入：tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
输出：2
解释： 
图一表示：在我们旋转之前， tops 和 bottoms 给出的多米诺牌。 
如果我们旋转第二个和第四个多米诺骨牌，我们可以使上面一行中的每个值都等于 2，如图二所示。

示例 2：

1
2
3

输入：tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
输出：-1
解释： 在这种情况下，不可能旋转多米诺牌使一行的值相等。

提示：

2 <= tops.length <= 2 * 104
bottoms.length == tops.length
1 <= tops[i], bottoms[i] <= 6

题解

暴力解法。首先遍历tops和bottoms两个数组，记录下两个数组中的数字1-6出现的次数。能够符合条件的数组，相同数字出现的次数之和一定大于数组长度，否则返回-1。

对于符合条件的数组，按照上述筛选出的符合条件的数字进行遍历：

遍历top，若top中的数字不是上述符合条件的数字，则验证bottom是否符合，不符合则返回-1，符合则step+1，记录下所有step；
遍历bottoms，重复针对tops的操作；
针对上述两次遍历的所有step，找出其中除-1外的最小值，否则返回-1。

class Solution:
    def minDominoRotations(self, tops: list[int], bottoms: list[int]) -> int:
        length = len(tops)
        top_dict = {1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0}
        bottom_dict = {1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0}
        for top in tops:
            top_dict[top] += 1
        for bottom in bottoms:
            bottom_dict[bottom] += 1
        # max_top, max_bottom = -1, -1
        okay_lst = []
        flag = False
        for i in range(1, 7):
            if top_dict[i] + bottom_dict[i] >= length:
                flag = True
                okay_lst.append(i)
        if not flag:
            return -1
        ret_lst = [0 for _ in range(2 * len(okay_lst))]
        for i in range(len(okay_lst)):
            for j in range(0, len(bottoms)):
                if bottoms[j] != okay_lst[i]:
                    if tops[j] != okay_lst[i]:
                        ret_lst[i] = -1
                        break
                    else:
                        ret_lst[i] += 1
        for i in range(len(okay_lst)):
            for j in range(0, len(bottoms)):
                if tops[j] != okay_lst[i]:
                    if bottoms[j] != okay_lst[i]:
                        ret_lst[i + len(okay_lst)] = -1
                        break
                    else:
                        ret_lst[i + len(okay_lst)] += 1

        min_step = 2147483647
        ret_flag = False
        for step in ret_lst:
            if step != -1:
                min_step = min(min_step, step)
                ret_flag = True
        return min_step if ret_flag else -1


if __name__ == '__main__':
    s = Solution()
    print(s.minDominoRotations( [2,1,2,4,2,2],  [5,2,6,2,3,2]))

提交记录

https://leetcode.cn/problems/minimum-domino-rotations-for-equal-row/submissions/627154458

GONEVMYS

leetcode每日一题——1007. 行相等的最少多米诺旋转

1007. 行相等的最少多米诺旋转

题解

提交记录